Энергетическая яркость
Все формы облучённости сочетают в себе свет, идущий с многих направлений. Помимо некоторых простых ситуаций, не имеет значения, откуда исходит фотон. Однако предположим, что вам нужно знать яркость определенного места – например, угол крыла бабочки или подгрудка ящерицы. Здесь вам нужно использовать энергетическую яркость (лучистость). Как и облучённость, энергетическая яркость определяется тем, сколько фотонов попадают на небольшую поверхность за определенный промежуток времени, но в этом случае учитываются только фотоны, которые поступают из ограниченного количества направлений. Кроме того, количество фотонов, поступающих из заданного направления делится на угловой размер просматриваемой области. Это подводит нас к одному из наиболее устрашающих аспектов измерения света – стерадиану.
Стерадиан (ср), является единицей телесного угла, а сам телесный угол является двумерным аналогом обычного геометрического угла (рисунок 2.6).
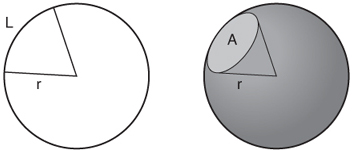
Солидную часть моей жизни стерадиан смущал меня (я притворялся что это не так, но не помогало), пока, наконец, я не выработал эту воображаемую картину. Представьте себе круг. Из геометрии средней школы известно, что его окружность равна 2πr, где r - радиус. Отношение окружности этого круга к его радиусу составляет 2π. Вот почему мы говорим, что 360 градусов равны 2π радианам (и почему один радиан примерно равен довольно неуклюжему значению 57.2958°). Добавьте пространственное измерение и представьте сферу. Её площадь поверхности 4πr2, поэтому отношение площади поверхности к квадрату радиуса 4π. Поэтому мы говорим, что полная сфера равна 4π стерадиана.
Теперь представьте, что вы смотрите на синего краба, плывущего рядом с вами в океане. В зависимости от его ориентации и формы, краб имеет определенную площадь поперечного сечения, если смотреть с вашей точки обзора. Телесный угол краба в стерадианах – это площадь поперечного сечения, разделенная на квадрат расстояния между ним и вами. Энергетическая яркость краба – это количество света, которое отражается от него и попадает в детектор (за определённый период времени и разделённое на размер детектора), делённое на телесный угол краба. Поскольку полное 3D-поле зрения - 4π стерадиан, один стерадиан - около 8% сферы (примерно часть земного шара, который занимает Азия). Это также равно примерно 3283 квадратных градусам, но телесные углы редко измеряются таким образом.
Объекты редко имеют один цвет и яркость, поэтому большую часть времени вы измеряете энергетическую яркость определённой площади на объекте, а не всего объекта целиком. В этом случае используемый в измерениях телесный угол определяется полем зрения вашего детектора. Это поле зрения обычно можно определить с помощью некоторой тригонометрии. Например, маленький детектор расположен на одном конце трубки диаметром 4 см и длиной 20 см, и имеет поле зрения примерно π22/202 или около 0,03 ср (рисунок 2.7). В основе всего этого лежит невысказанное предположение, что поле зрения примерно круговое или, по крайней мере, квадратное. Если ваш детектор фиксирует в пространстве большую фигуру с неровными краями, я не уверен, что вы измеряете, но это не энергетическая яркость.

Сохранение энергетической яркости
Возможно, наиболее часто цитируемым оптическим законом является закон обратных квадратов – освещённость объекта уменьшается пропорционально квадрату расстояния от источника света. Даже люди, визуально наблюдающие, что их друзья не становятся темнее по мере того как отходят дальше, всё равно включают закон обратных квадратов в свои статьи. Это классический пример веры в то, что математическая модель предпочтительней непосредственного опыта.
Для энергетической яркости закон обратных квадратов почти всегда ошибочен. Следующее объяснение, основанное на главе из книги Борена «Облака в стакане пива» объясняет почему. Предположим, в холодную ночь вы стоите в пяти метрах от небольшого костра. Ваша кожа, весьма хороший детектор облучённости, ощущает комбинацию тепла огня и окружающего воздуха. Ваш глаз, великолепный детектор энергетической яркости, измеряет энергетическую яркость огня относительно темного фона. Затем вы отходите ещё на пять метров, и расстояние между вами и костром составляет десять метров. Что произойдёт с облучённостью и энергетической яркостью? Предположим, что костёр излучает фотоны равномерно во всех направлениях. С точки зрения костра телесный угол вашего тела (угол зрения) составляет лишь четверть от того, каким он был до вашего перемещения. Так как вы удалились в два раза, вы будете в два раза меньше как в ширину, так и высоту для наблюдателя, находящегося в костре. Поскольку ваше тело получает только четверть фотонов, то и облучённость будет составлять только четверть от предыдущего значения. На уровне личных ощущений ваша кожа ощутит тепло огня только на четверть от предыдущего. Для облучённости закон обратных квадратов работает, и это знает любой, проведший достаточно времени вокруг костров.
Но что насчёт энергетической яркости? Как и в случае тела, с точки зрения огня телесный угол вашего зрачка составляет только четверть от того, что было раньше, и перехватывает только четвёртую часть фотонов. Однако, поскольку вы отдалились, огонь кажется меньше. Фактически, огонь сам имеет только четверть от предыдущего телесного угла, и в два раза меньше по ширине и высоте. И поскольку для определения энергетической яркости необходимо разделить количество фотонов на телесный угол, то значение не изменяется. Этот простой геометрический принцип лежит в основе того, что называется «сохранением энергетической яркости».
Есть, однако, три оговорки. Во-первых, промежуточная среда должна быть «без потерь», что означает, что она не поглощает и не рассеивает свет. Чистый воздух является средой без потерь на довольно больших расстояниях, но не в случае тумана или дымки над отдаленными горами. Это означает, что значение энергетической яркость приблизительно одинаково у лампочки через дорогу, и лампочки у вас в руках. Поскольку космическое пространство мало влияет на распространение света, то солнце, наблюдаемое с Плутона, будет иметь такую же энергетическую яркость, как и с Земли. Оно будет выглядеть намного меньше, но останется таким же ярким. Вода не является средой без потерь, поэтому энергетическая яркость сохраняется только на коротких расстояниях и только в самых чистых средах обитания.
Вторая оговорка связана с вопросом, который, возможно, уже приходил в голову – если энергетическая яркость сохраняется, то почему более отдаленные звезды тускнеют? В некоторых случаях это происходит из-за воздействия пыли, поглощающей свет, но гораздо важнее то, что звёзды по существу являются точечными источниками излучения. Даже самая близкая к нам яркая звезда, Альфа Центавра, имеет телесный угол только 2 миллионных долей градуса, что примерно составляет 1/4000-й телесного угла самого маленького объекта, который мы можем зафиксировать. Таким образом, мы фактически не видим эту или любую звезду, вместо этого мы видим их дифракционные картины. Мы поговорим об этом позже, но пока важно отметить что, когда звезда удаляется, количество фотонов света от неё, попадающих в наш зрачок, уменьшается, но сам образ звезды не уменьшается. Так как нет никакого баланса между количеством полученных фотонов и телесным углом расстояния до звезды, яркость уменьшается согласно закону обратных квадратов. Таким образом, вторая оговорка: энергетическая яркость сохраняется только в том случае, если рассматриваемый объект не сжимается до точки.
Но как мы решим, что некий объект является точкой? Очевидно, что даже звезды не являются бесконечно малыми геометрическими точками. Хотя похоже, что мы могли бы принять произвольное решение, на самом деле существует четкое разделение между протяжёнными объектами, энергетическая яркость которых сохраняется, и точечными объектами, где яркость падает согласно закону обратных квадратов. Всё зависит от детектора. Если телесный угол объекта ниже предела разрешения детектора, то он является точечным источником; если он выше этого предела, то это протяжённый объект.
В некотором роде это стыд, поскольку результаты измерения энергетической яркости, в отличие от облучённости, зависят от того, кто и чем их измеряет. Довольно расплывчато для физического свойства. Например, острота зрения орлов примерно в два раза превышает человеческую. Если бы вы продолжили бы отходить от костра, о котором мы говорили в примере, но на плече у вас сидел бы орёл, костёр стал бы точечным источником света сначала для вас, а потом для птицы. После этого момента, и до тех пор, пока он не станет точечным источником для орла, огонь будет тускнеть для вас с увеличением расстояния, но останется на той же яркости для птицы. Однако, вы будете согласны с птицей по поводу того, насколько меньше костёр стал греть вас.
Интересна третья и последняя оговорка. Если вы когда-либо занимались подводным плаваньем, то замечали (или вам говорили обратить внимание), что вещи под водой часто выглядят больше, чем в действительности. Это происходит потому что свет преломляется на поверхности вашей маски, и движется из водной среды в воздушную (короткое путешествие через стекло самой маски можно игнорировать). Преломление оказывается гораздо более интересным, чем вы могли бы ожидать, мы обсудим это далее в главе 6. Пока же давайте просто скажем что свет резко изгибается всякий раз, когда он перемещается в среду с другим показателем преломления. Из-за этого изгиба подводный объект, просматриваемый во время погружения через маску, выглядит больше (рисунок 2.8). Насколько данный объект будет казаться больше зависит его размера, и от того, насколько он далеко в сравнении с тем, насколько далеко ваши глаза от стекла маски. При условии что расстояние между стеклом маски и глазами обычно составляет 3 см, объект, отдалённый более чем на 50 см и менее 15° в поперечнике углового диаметра, на 33% шире и на 33% выше. Подумайте об этом как «больше в 1,33 раза», и тут должен зазвонить колокольчик. Да, увеличение равно показателю преломления воды (= 1,33), деленному на показатель преломления воздуха (= 1).
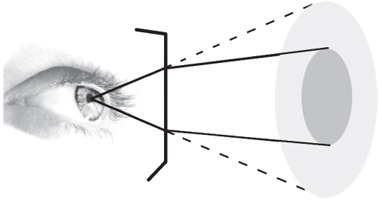
Поскольку площадь равна квадрату длины, телесный угол объектов, находящихся под водой, увеличивается с коэффициентом m2, где m - отношение индексов двух сред (1,332 ≈ 1,75 для воды, наблюдаемой через воздух вашей маски). Но общее количество фотонов, которые достигают вашего глаза от объекта, не изменилось (оно не может не нарушать фундаментальные законы сохранения). Энергетическая яркость – это общее количество фотонов, деленное на телесный угол, поэтому яркость объекта уменьшается с коэффициентом m2. Другими словами, объекты, находящиеся под водой, выглядят больше и тусклее.
Если вы не ныряете как ищейка, уткнувшись носом в риф, то большинство видимых объектов будут на расстоянии больше 50-ти см. Кроме того, большинство объектов будет меньше 15° в поперечнике. Однако, чтобы закрыть тему, мы должны подумать о том, что происходит для более близко расположенных объектов, и составляющих более 15° в поперечнике. По мере приближения объекта к маске его увеличение уменьшается до тех пор, пока он не коснётся маски и примет истинный размер. Попробуйте проделать это под водой в следующий раз, когда вы займётесь подводным плаваньем. Если погружения вас не интересуют, то тот же эффект можно наблюдать, погрузив руку в аквариум. Что касается больших объектов (и под «большими», я имею в виду большие по угловому, а не реальному размеру), то их края увеличиваются более чем в 2 раза, поэтому они начинают выглядеть растянутыми и искаженными (рисунок 2.9).

А что происходит с яркостью на этих близких расстояниях и/или больших угловых размерах? Она всё ещё падает с коэффициентом m2? Удивительно, но это так, хотя увеличение не всегда равно m2. Это может быть доказано математически или экспериментально, но, к сожалению, я не могу предложить хорошее интуитивное объяснение. Основная причина заключается в том, что яркость также зависит от угла между светом и детектором, который изменяется при пересечении сред воздух-вода. Оказывается, эта коррекция совершенно отменяет вариации в увеличении изображения и оставляет только коэффициент m2.
Конечным результатом всего этого является то, что сохраняется не ярость, а яркость, делённая на m2. Возвращаясь к нашему ныряльщику, представим, что другой человек сидит в маленькой лодке и светит не него через воду лучом фонаря. Игнорируя обычные единицы, представим, что фонарик излучает луч, яркость которого в воздухе составляет одну единицу. Когда луч попадает в воду, его яркость подпрыгивает до 1,75 (= 1,332). Это то, что ныряльщик увидит, если у него/неё нет маски. Тем не менее, дайвинг без маски делает человека ужасно дальнозорким, поэтому давайте вернем её на место. Сама маска изготовлена из стекла с индексом преломления около 1,5. Таким образом, после короткого путешествии светового луча через стекло маски яркость прыгает до 2,25. Затем луч сталкивается с воздухом между маской и глазом ныряльщика, и яркость возвращается к единице. Так что если ныряльщик одет в маску, под водой свет фонарика выглядит не ярче или тусклее, чем если бы он или она сидели с другом в лодке. В некоторых случаях, однако, яркость действительно меняется: например, ныряльщик смотрит на подводные объекты и видит, что они больше и тусклее. Другой случай включает диффузно отражающие (например, неблестящие) объекты в воде, которые освещены и наблюдаются сверху из воздушной среды. Bohren и Clothiaux (2006) демонстрируют хорошую фотографию, показывающую, что белые пластиковые ложки в чёрных наполненных водой чашах выглядят темнее. Вы можете увидеть тот же эффект, если опустите руки в пруд с тёмным дном. Я лично считаю увлекательным, что относительно отвлечённые геометрические дискуссии иногда подтверждаются простыми наблюдаемыми последствиями.
Было бы неплохо закончить главу на этой высокой ноте, но я чувствую, что мне всё же нужно обратиться к фотометрическим единицам.

