Поляризация
Беритесь за проект только если он заведомо важный и практически невыполнимый.
– Эдвин Лэнд (из «Защита Эдвина Лэнда», Форбс)
Эдвин Лэнд был выдающимся человеком. Хотя он так никогда и не закончил колледж, Лэнд был доминирующей фигурой в области фотографии и оптики на протяжении большей части двадцатого века, и внёс фундаментальный вклад в понимание цветового зрения. Двумя его самыми известными изобретениями были камера Polaroid и поляризационный фильтр. Последний, созданный поздно ночью с использованием оборудования и площадей, без спроса заимствованных в Колумбийском университете, нашёл себе применение для бесчисленных технических и научных задач, начиная от 3D-фильмов и заканчивая изучением навигации пчёл. Разговор о поляризации света стоило начать с вдохновляющего, и отчасти пугающего примера Эдвина Лэнда.
Как и в случае радиометрии, поляризация может быть сбивающей с толку темой. К сожалению, в отличие от радиометрии, её сложность в основном происходит не из-за путаницы единиц измерений. Физика поляризованного света действительно сложна. Это еще одна сфера оптики, в которой о свете проще думать, как о волне. Если хотите, можете представить, что отдельные фотоны имеют поляризацию, и сделать это отправной точкой ваших рассуждений, но поверьте, лучше вам этого не хотеть.
Поскольку поляризация часто не очень удачно описывается, я начну главу с того, что как я надеюсь, представляет собой ясное введение в эту тему. Разговор будет немного абстрактным, но потерпите немного. Дальше по главе мы познакомимся с интересной феноменологией этого предмета (в том числе танцующими пчёлами и катящимся навозом).
Виды поляризации
Помните, что о свете можно думать как о волне, распространяющейся в пространстве. Теперь представьте себе совершенно монохроматический, идеально коллимированный (весь свет движется строго параллельно) луч света в идеальном вакууме (оптика полна платонических идеалов). Если вы держите небольшой измеритель электрического поля на пути этого луча, он показывает, что величина локального электрического поля очень сильно изменяется синусоидально (мы допускаем, что счётчик может улавливать столь быстрые изменения, чего он, вероятно, не может). Но как насчет направления поля? В отличие от давления воздуха для звуковой волны, электрические поля являются векторами и, следовательно, имеют как величину, так и направление. Это направление для наших целей всегда перпендикулярно направлению распространения светового луча и называется «e-вектором». E-вектор обозначается углом, обычно относительно вертикали (хотя любой угол возможен) (рис. 8.1).
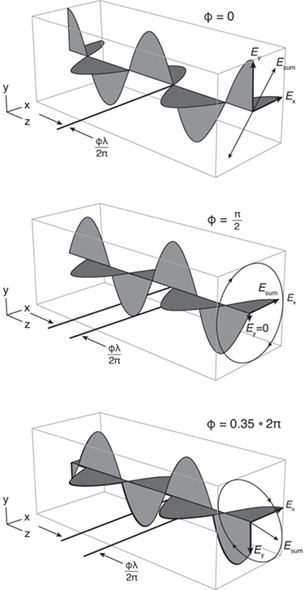
Вы могли заметить, что я не упомянул магнитное поле. Поскольку магнитное поле обычно (но не всегда) перпендикулярно и в фазе с электрическим полем, e-вектор указывает вам вектор магнитного поля. В большинстве случаев электрическое поле оказывает гораздо большее влияние на вещество, поэтому обычно поляризация описывается по e-вектору, хотя в некоторых странах ученые предпочитают использовать вектор магнитного поля.
Как и все векторы, e-вектор можно разбить на две перпендикулярных компонента, которые могут быть под любым углом, хотя часто проще всего использовать горизонтальные и вертикальные, что мы сделаем здесь. Таким образом, любой монохроматический параллельный луч света можно рассматривать как сумму двух лучей, один с горизонтальным e-вектором, и один с вертикальным e-вектором. Конечно, только потому, что можно что-то сделать, это не значит, что нужно делать. Что мы получаем взамен? Довольно хороший способ взглянуть на поляризованный свет.
Как и все простые волны, горизонтальная и вертикальная составляющие e-вектора полностью описываются тремя вещами: частотой, амплитудой и фазой. Мы сказали, что наш луч монохроматичен, поэтому мы можем игнорировать частоту. На самом деле, давайте просто примем её за единицу. Абсолютные фазы нам также не интересны, только разность фаз между двумя лучами. Таким образом, установим фазу горизонтальной составляющей равную нулю. После этих упрощений горизонтальная и вертикальная составляющие электрического поля, измеренные нашим маленьким счетчиком, составляют:
8.1
где t – время, Ah и Av - амплитуды горизонтально и вертикально поляризованных компонентов, φ - разность фаз между ними. Что происходит с электрическим полем с течением времени? Если разность фаз φ равна нулю, то `E _( v ) = ( A _( v ))/( A _( h )) E _( h )`, что означает, что амплитуда вертикального поля – это только восьмая часть горизонтального поля, поэтому угол e-вектора никогда не изменяется, за исключением того, что идёт в противоположном направлении в течение половины цикла. Если Av равно нулю, то Ev также всегда равно нулю, поэтому e-вектор является горизонтальным. Если Ah равно нулю, то e-вектор является вертикальным. Если оба они равны нулю, то света нет вообще. В общем случае угол e-вектора является арктангенсом `( A _( h ))/( A _( v ))`.
Мы только что описали линейно поляризованный свет. Прежде чем двигаться дальше, есть небольшая проблема. E-векторные углы составляют только от 0 ° до 180 °, а не от 0 ° до 360 °. Это связано с тем, что они указывают в противоположных направлениях, в зависимости от текущей фазы волны. Таким образом, понятно, что углы e-вектора θ и 180 ° + θ одинаковы. Фактически, в общем случае электронный вектор не является вектором, а осью. Названия никогда не означают именно то, что вы от них хотите. Некоторые люди предпочитают использовать «угол поляризации» или более точный термин «ось поляризации», но «e-вектор» доминирует в научных статьях, поэтому мы будем придерживаться его. Однако я добавлю «ось», чтобы было ясно, что он указывает в оба направления.
Я знаю, что всё выглядит будто мы использовали пушку, чтобы выбить и так открытую дверь, но это оттого, что линейная поляризация является лишь ограниченным случаем более общего явления. Предположим, что разность фаз φ в уравнении 8.1 не равна нулю. Тогда конечная точка вектора электрического поля, вместо того чтобы просто складываться то внутрь, то наружу и обратно на одной оси, рисует кривую. Другими словами, ось e-вектора изменяется со временем, но предсказуемым образом. В общем случае, кривая рисует эллипс, форма и ориентация которого зависит от разности фаз между двумя компонентами и их относительной амплитуды (рис. 8.1). Геометрически линия может рассматриваться как плоский эллипс, поэтому ось линейной поляризации также является эллипсом. Думайте об этом как об ограниченном случае.
Другим ограниченным случаем эллипса является круг. Это происходит, когда Ah = Av и разность фаз между двумя компонентами составляет 90° или -90°. Этот особый случай, когда вектор электрического поля описывает идеальный круг 1014 раз в секунду (для видимого света), называется «круговой поляризацией». Если разность фаз равна 90°, то поляризация называется «правой», потому что, если бы вы могли остановить время, спиральная траектория e-вектора вектора была бы похожа на резьбу на типичном винте с правой нарезкой (его иногда называют «по часовой стрелке» или «правой круговой» поляризаций). Если разность фаз составляет -90°, поляризация называется «левой круговой» поляризацией или «против часовой стрелки». Если только вы не инженер-электрик, иначе наименования меняются на противоположные. Честно говоря, каждый раз, когда появляются термины «правые» и «левые» в физике и технике, у меня начинает болеть голова. Обычно нужно смотреть, что касается вашей конкретной системы, забыть это, смотреть снова, забыть об этом и так далее.
Круговая и эллиптическая поляризация могут казаться вещами не от мира сего. Кого волнует, если вектор электрического поля описывает круг или эллипс 1014 раз в секунду? Кто может это увидеть? Оказывается, однако, что свет круговой поляризации встречается в природе, и что некоторые животные действительно могут видеть и использовать его. Подробнее об этом позже. Сначала нам нужно покинуть идиллический вымышленный мир совершенных волн, и обратиться к изменчивой реальности.

