Фотометрические единицы
Фотометрические единицы основаны на зрительном восприятии человека, и получены из десятилетий экспериментов в человеческой психофизике, но в силу этого являются необоснованными, когда речь идет о нечеловеческих визуальных системах. Кроме того, как я упоминал во введении, фотометрические единицы – это кошмар. Если вам мало фут-ламберта и нит, попробуйте добавить апостильб, скот и миллиблондель (тысяча маленьких блондинок?). Тем не менее, по своей сути фотометрия основана на факте, который полезен для биологов, – что зрение и другие биологические процессы не одинаково эффективны на всех длинах волн света. Даже в пределах видимого диапазона человеческие глаза гораздо более чувствительны к свету 555 нм, чем свету на 410 нм, поэтому жёлтый цвет выглядит ярче, чем фиолетовый. Поэтому, хоть я и рекомендовал бы отбросить эти единицы (за исключением работы в визуальной психофизике человека), общий принцип стоит помнить.
Математическая реализация этой идеи известна как «взвешенный интеграл». Всё начинается с измерения спектра освещённости или энергетической яркости, затем значения для каждой длины волны умножаются на функцию, соответствующую чувствительности данного глаза (или любого другого биологического процесса), а затем интегрируются. В виде уравнения взвешенный интеграл w равен:
2.2
Где λ1 и λ2 определяют диапазон длин волн (от 380 нм до 760 нм для дневного зрения человека), Eλ представляет собой измеренную яркость или облучённость в фотонах или ваттах, а Vλ - функция чувствительности (либо на ватт, либо на фотон) (рисунок 2.10).
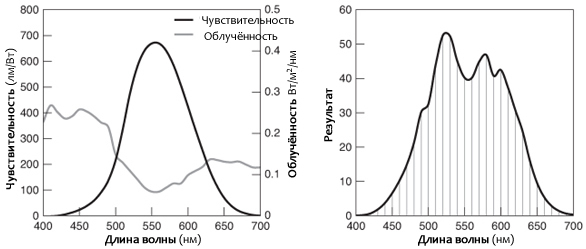
Помните, что функция чувствительности должна находиться в тех же единицах, что и спектр. На практике этот взвешенный интеграл обычно выполняется в Excel или Matlab с дискретными интервалами длины волны Δλ не менее 5 нм. Другими словами:
2.3
Vλ обычно представляет собой спектральную чувствительность некоторого фоторецептора, определяемую с помощью микроспектрофотометрии или спектральной чувствительности всего глаза с использованием электроретинографии. Имея некоторые знания о визуальной системе вида, с которым вы работаете, вы можете использовать эти формулы чтобы определить, насколько ярким будет объект для этого животного. Если у животного есть фоторецепторы нескольких классов, вы можете определить относительное возбуждение каждого и получить впечатление о восприятии цвета. Тот же процесс часто используется для оценки воздействия ультрафиолетового излучения, фотоактивного излучения, и в других ситуациях, когда речь идет о процессе, зависящем от длины волны.
Большая разница между описанным мной методом и классической фотометрией заключается в том, что вы начинаете с измерения всего спектра, а затем вычисляете интегрированное значение. Напротив, фотометрические датчики обычно имеют фильтры, которые имитируют спектральную чувствительность глаза человека и, таким образом, выполняют всю интеграцию внутри инструмента. Добавлять числа для выведения общей суммы является тривиальной задачей, но невозможно восстановить числа, если есть только интегрированная сумма. Поэтому, если у вас есть фотометр, дающий только интегрированные фотометрические значения, продайте его и купите спектрометр.
Что делать, если вам нужно использовать чужие данные, и они в фотометрических единицах? Можно преобразовать их в фотоны, если известна основная форма спектра. Функция спектральной чувствительности для фотометрических единиц человеческого зрения может быть найдена во многих местах (и в приложении A этой книги). Учитывая это и основную форму спектра измеренного света, можно работать в обратном направлении из уравнения 2.3 и определить, сколько фотонов имеется на каждой длине волны. Существуют простые программные способы сделать это, но я обычно настраиваю электронную таблицу, где измеренный спектр умножается на какое-то произвольное значение, а затем меняю это значение, пока интеграл, взвешенный по фотометрической функции, не совпадёт с измеренным фотометрическим значением.
Изначальное и правильное использование фотометрических единиц состоит в том, чтобы преобразовать целый спектр в одно число, являющееся оценкой того, насколько ярким свет кажется людям. Предположим, ваша задача состоит в том, чтобы показать, как освещённость изменяется в течении дня с интервалами в 10 минут. Можно собрать сотни спектров в каком-то одном трёхмерном представлении, но эти данные занимают много места и их трудно интерпретировать. Если всё, о чем вы заботитесь, это общий уровень освещенности, тогда не стесняйтесь давать его в фотометрических единицах (или в аналогичных единицах, подходящих для визуальной системы вашего животного).
Фотометрическим аналогом облучённости является освещённость, она имеет свою единицу измерения в системе СИ, называющуюся «люкс» Люкс – это люмен, делённый на м2. Люмен – это одна кандела, умноженная на телесный угол, выраженный в стерадианах. Сама кандела берёт начало из «силы в свечах», и является объёмом света, производимым чистой спермацетовой свечой весом в одну шестую часть фунта и сгорающей со скоростью 120 зерен на час. Вы можете понять, почему я призываю вас держаться подальше ото всех этих единиц.
Как бы то ни было, я буду использовать «люкс» в дальнейшем, и в приложении A дан метод конвертации спектра в люкс. Таблица 2.1 даст вам представление о размерности этой единицы. Также существует единица «яркость», которая является фотометрическим аналогом энергетической яркости, и троланд, единица, берущая в расчёт площадь зрачка человеческого глаза, но они ещё более специфичны для исследований человеческого зрения.
| Таблица 2.1. Освещённость при различных условиях (в люкс) | |
|---|---|
| Дневной свет (с прямым солнечным светом) | 100 000 |
| Дневной свет (без прямого солнечного света) | 10 000 |
| Пасмурный день | 1000 |
| Очень пасмурный день | 100 |
| Поздние гражданские сумерки | 10 |
| Поздние навигационные сумерки | 1 |
| Полнолуние | 0.1 |
| Серп луны | 0.01 |
| Безлунная ночь (ясное небо) | 0.001 |
| Безлунная ночь (пасмурно) | 0.0001 |
И ещё кое-что о фотометрических единицах. Фотометрическая яркость – это не одно и тоже, что и яркость цветовосприятия. Другими словами, только потому, что две области имеют одинаковую яркость, это не значит, что они кажутся одинаково яркими для глаза. Наш мозг настраивает изображение несколькими способами, прежде чем мы действительно его воспринимаем. Одна из теорий, разработанная Дейлом Пурвесом, заключается в том, что это делается для минимизации на наше восприятие мира путающих эффектов теней, дымки и изменения освещения (Purves and Lotto, 2003). У других исследователей есть другие гипотезы, но, независимо от причин, эффекты сильны (рис. 2.11).
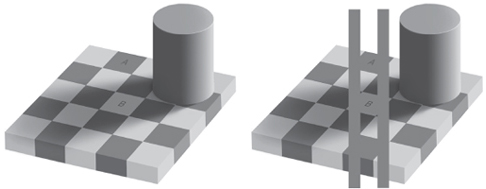
Кроме того, никто иной как авторитет Оптического общество Америки утверждает, что даже изолированные монохроматические источники света той же яркости не кажутся одинаково яркими. Например, фиолетовый свет будет казаться ярче жёлтого света той же яркости (Smith and Pokorny, 2003). Но разве светимость не основана на воспринимаемой интенсивности монохроматического источника света, и не должны ли все монохроматические источники с одним показателем яркости светового потока иметь одну яркость цветовосприятия? Это меня беспокоит.
В заключение
Жаль, что запутанная геометрия и разросшиеся единицы измерения удерживают так много людей от оптики. Для биологов, не изучающих людей, оптика сводится к нескольким простым правилам. (1) Используйте фотоны, а не ватты. (2) Используйте длину волны, а не частоту, но будьте предельно осторожны при сравнении пиков спектров света с кривыми чувствительности. (3) Придерживайтесь измерения облучённости и энергетической яркости, но будьте пионером и добавьте измерения скалярной облучённости в свои работы. (3) Иногда облучённость подчиняется закону обратного квадратов расстояний; энергетическая яркость делает это редко. (4) Не используйте фотометрических единиц, за исключением, возможно, люкса. Избегайте даже читать о них. Однако основополагающий принцип взвешенных интегралов полезен для моделирования зрения животных и других зависимых от длины волны процессов.

