Как измеряется рассеяние света
Прежде чем начать рассматривать случаи рассеяния света, нам нужно поговорить о том, как оно характеризуется. Хотя физики рассматривают рассеяние по-разному, в том числе и с использованием малоприятных тензорных вычислений, для биологов наиболее полезны три характеристики: (1) коэффициент рассеяния, (2) эффективное поперечное сечение и (3) параметр асимметрии. Коэффициент рассеяния – это аналог коэффициента поглощения, рассмотренного в предыдущей главе, и он также прост в использовании. Его размерностью является обратное расстояние, обычно он обозначается буквой b и указывает скорость, с которой рассеивается свет. Таким образом, в непоглощающей системе, освещенной лучом света, количество нерассеянного света, всё ещё находящегося в луче после того, как он прошёл расстояние d, равно:
5.1
где Io - первоначальная интенсивность луча. Таким образом количество рассеянного света равно:
5.2
Вспоминая, что мы использовали a для коэффициента поглощения в главе 4, количество света в луче, который не рассеивается и не поглощается, составляет:
5.3
где c (которое равно a + b) называется либо «коэффициентом затухания луча», либо «коэффициентом экстинкции». Этот термин оказывается полезным, когда вы хотите выяснить, как что-то растворяется в фоне при наблюдении через мутную среду, такую как туман или вода. Фактически, почти все исследования видимости имеют дело с c, оттого это стоит помнить.
Проблема с коэффициентом рассеяния заключается в том, что вы должны измерять его напрямую с помощью дорогостоящего оборудования. Поскольку он обычно зависит от слишком большого числа параметров, за исключением некоторых простых случаев его трудно определить другими способами. Он также мало сообщает о том, как размер и форма частиц среды влияют на количество рассеянного света, и куда свет движется.
Чтобы лучше понять эти две вещи, необходимо работать с эффективным поперечным сечением и фазовыми функциями. Первое довольно просто. Представьте себе параллельный луч света, направленный на непоглощающую частицу. Часть этого света будет рассеиваться и, таким образом, покидать луч. Теперь рассмотрим непрозрачный диск, площадь поперечного сечения которого такова, что если он помещен в луч, он будет закрывать рассеянный частицей свет. Площадь этого диска – это эффективное (рассеивающее) поперечное сечение частицы (обычно называемое «Csca»). Разделение эффективного поперечного сечения на фактическую площадь поперечного сечения частицы дает еще один полезный термин – эффективность рассеяния (так называемая «Qsca»). Он говорит о том, насколько хороша частица в рассеянии света.
Фазовая функция сообщает, сколько света рассеивается во всех направлениях. Несмотря на свое название, он ничего не говорит о фазе световой волны. Эта функция часто нормализуется по общему количеству света, рассеянного во всех направлениях, поскольку людей, как правило, больше интересует относительное распределение рассеянного света, чем его абсолютная интенсивность. Вы можете рассчитать фактическое количество рассеянного света в каждом направлении путём умножения эффективного поперечного сечение и интенсивности падающего света.
По крайней мере 99% биологов, скорее всего, никогда не будут использовать фазовые функции напрямую, но существует грубое, но красивое упрощение, в краткой форме показывающее, как рассеивается свет. Известное как «параметр асимметрии» (и странно обозначаемое g), оно представляет собой средневзвешенное по косинусу значение фазовой функции. Обратный косинус этого числа примерно покажет вам средний угол, по которому рассеивается свет. Например, g единицы означает, что весь свет рассеивается прямо вперед, g -1 означает, что весь свет рассеивается прямо назад. Значение g 0 означает, что в переднем полушарии света рассеивается столько же, как и в обратном полушарии. Более конкретный пример – g для кристаллов льда в перистых облаках составляет около 0,7. Это означает, что около половины рассеянного света находится в переднем конусе с половинным углом 46°. Поскольку g примерно сообщает, сколько света рассеивается вперед и назад, оно используется во всех видах простых, но довольно точных моделей распространения света через плотные беспорядочные вещества, такие как биологические ткани.
И хотя детали могут быть сложными, только три вещи влияют на то, насколько эффективно отдельно взятая частица рассеивает свет: (1) её размер относительно попадающей на неё длины волны света, (2) её показатель преломления относительно показателя преломления окружающей среды, и – в гораздо меньшей степени – (3) форма частицы. Абсолютный размер и показатель преломления частицы не имеют значения. Поэтому, если относительные показатели одинаковы, мрамор шириной в 2 см рассеивает микроволны с длиной волны 1 сантиметр так же эффективно и с тем же угловым распространением, как и липидная везикула шириной 1 мкм рассеивает зелёный свет с длиной волны 500 нм. И в результате, если вы сможете подобрать материалы с подходящими показателями преломления, вы сможете моделировать рассеяние света в живой клетке используя пластиковую модель и микроволновку. Аналогично, кубик диоксида циркония (n = 2,2) в воде (n = 1,33) рассеивает свет точно так же, как идентичный кусочек стекла (n = 1,51) на воздухе (n = 1). Абсолютный индекс среды имеет значение косвенным образом, поскольку он влияет на длину волны падающего света. Действительно критическим является размер частицы, поэтому в следующих трех разделах рассматривается рассеяние от частиц с диаметрами намного меньше, намного больше или примерно такого же размера, как и длина волны падающего света.
Малые частицы
В случае частиц с радиусами менее 10% длины волны света, все части частицы воспринимают падающий луч света как имеющий одну и ту же фазу и интенсивность. Таким образом, весь излучаемый ими рассеянный свет более или менее в фазе, что означает, что вы можете складывать высоты каждой волны, рассеянной от части частицы, не беспокоясь о интерференции волн. Поскольку энергия волны пропорциональна квадрату высоты волны, для малых частиц рассеяние быстро растет с размером частицы. Действительно, для малых частиц эффективность рассеяния пропорциональна четвертой степени радиуса частицы (относительно длины волны):
5.4
Так как эффективное поперечное сечение частицы Csca – это просто эффективность, умноженная на физическое поперечное сечение, мы получаем удобное уравнение:
5.5
где V - объем частицы. Таким образом, для малых частиц – белков, рибосом и т.д. рассеяние пропорционально квадрату объема. Вы, наверное, заметили, что я принимаю частицу за сферу. Это связано с тем, что, если относительный показатель преломления не достигает больших величин (больше, чем можно найти в биологии), форма мелких частиц оказывает на рассеяние только умеренное влияние.
Несмотря на то, что для малых частиц рассеяние быстро растёт с возрастанием размера, оно чрезвычайно мало. Частицы малы относительно длины волны падающего света, и они рассевают свет очень слабо. Эффективность рассеяния глобулярного белка диаметром 10 нм в видимом спектре света составляет всего 5 × 10-7! Это означает, что он рассеивает такое же количество света, которое было бы закрыто диском всего на 0,007 нм в поперечнике (это около 14 атомов водорода, выстроенных в линию). Для сравнения, эффективность рассеяния стеклянного шарика диаметром 4 мкм в воде составляет около 3.
Значение λ4 в знаменателе отвечает за знаменитый факт, что мелкие частицы рассеивают голубой свет больше, чем красный, а это, по меньшей мере частично, отвечает за наше голубое небо и красное заходящее солнце, о чем будет сказано ниже. Помните, это не синий свет рассеивается легче, а конкретная частица по сравнению с синими волнами выглядит больше, а большие частицы рассеивают и больше света.
Итак, какую роль во всём этом играет показатель преломления? Если быть точным, эффективность рассеяния на малых частицах пропорциональна:
5.6
где m – отношение показателя преломления частицы и среды. Это довольно неуклюже. Однако большинство биологов, изучающих рассеяние, смотрят внутрь ткани или на частицы в воде. В этих случаях m близко к одному, и можно использовать более простое уравнение:
5.7
Даже для крайнего случая чистых частиц белка (n = 1,55) в воде отклонение будет составлять примерно 6-7%. Также из уравнения 5.7 можно увидеть, что не имеет значения, будет ли m больше или меньше единицы. Таким образом, липидная капля в цитоплазме рассеивает свет аналогично капле цитоплазмы в липиде. Вообще это справедливо и для более крупных частиц, что может помочь, когда вы думаете о вакуолях и других включениях с низким показателем преломления в клетках.
Как я упомянул в начале главы, что небольшие области материи рассеивают свет примерно одинаково во всех направлениях. Малые частицы делают то же самое. Точная функция фазы выглядит примерно как жирный арахис, с рассеянием в прямом и обратном направлениях вдвое большим, чем рассеянием по сторонам (рис. 5.3).
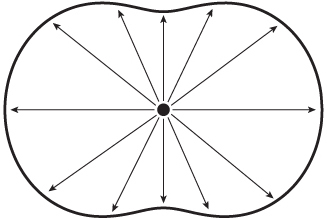
Это описывается относительно простым уравнением 1 + cos2θ, где θ - угол относительно направления вперёд (мы вернемся к этому уравнению, когда обсудим поляризацию в главе 8). Итак, если вы имеете дело с маленькими частицами, количество света, рассеянного в определенном направлении, следует этому соотношению:
5.8
Это уравнение описывает всё, что имеет значение для малых частиц с относительными показателями преломления, близкими к единице. Я оставил некоторые константы, которые можно найти в приложении F.
Большие частицы
В случае больших частиц рассеяние также является простым. Под «большими» подразумеваются частицы, имеющие радиус, по меньшей мере, в 100 раз превышающий длину волны (точный порог зависит от относительного показателя преломления). Например, для света на 500 нм мы говорим о чем-то размером, по крайней мере, 50 мкм, как диатомовая кремневая водоросль. Как только вы достигнете этих масштабов, произойдут две вещи. Во-первых, теперь вы можете использовать геометрическую оптику, чтобы выяснить, что происходит (трассировка лучей и т. д.). Что ещё лучше, эффективность рассеяния всегда равна двум. Другими словами, все большие частицы удаляют из луча столько света, сколько непрозрачный диск с двойной (относительно частицы) площадью поперечного сечения. Можно было бы подумать, что значение эффективности рассеяния равное единице будет иметь больше смысла, но оказывается, что крупные частицы влияют и на свет, который проходит рядом с ними, точно так же, как волны изгибаются, когда они огибают остров. Поэтому большие частицы фактически удаляют больше света из луча, чем можно предполагать по их тени.
Разумеется, фактическое количество рассеянного света зависит от ориентации частицы относительно светового луча. Стержень, расположенный параллельно лучу, рассеивает гораздо меньше света, чем расположенный перпендикулярно лучу, поскольку он имеет меньшее поперечное сечение. Но что если, как это часто бывает в биологии, мы не знаем ориентации? Или есть набор частиц, ориентированных во всех направлениях? В этом случае нам нужно было бы знать площадь поперечного сечения частицы, усредненную по всем ориентациям Aavg (другими словами, среднюю площадь её тени). Но здесь можно найти простой ответ. Пока твёрдое тело является выпуклым (т.е. в нём нет отверстий или больших выемок), его средняя площадь поперечного сечения составляет всего одну четверть площади поверхности Asurf. Таким образом, для больших частиц сечение рассеяния:
5.9
Поэтому объекты с большой площадью поверхности относительно их объема (например, плоские диски, длинные стержни) рассеивают много света на объем. Сферы, которые имеют самую низкую площадь поверхности для их объема, рассеивают наименьшее количество света на объем.
Средние частицы
Что насчёт частиц с радиусами более 1/10 длины волны падающего света и меньше 100 раз длины волны (для света 500 нм, частицы от 50 нм до 50 мкм в радиусе)? Многие важные компоненты клеток находятся в этом диапазоне: ядра, вакуоли, митохондрии, лизосомы и т.д. Печальная истина заключается в том, что в этом диапазоне трудно определить рассеяние, поскольку разные частицы испытывают разные фазы падающего света, и поскольку падающий свет изменяется путем его прохождения через частицу. Комбинация этих двух эффектов означает, что различные области частицы излучают рассеянный свет на разных фазах и амплитудах, и поэтому возникает множество сложных интерференций. В общем представлении, эффективность рассеяния по-прежнему увеличивается с увеличением размера частицы, но после преодоления некого порога размера частицы она фактически уменьшается. Когда это происходит, рассеяние начинает увеличиваться в зависимости от длины волны (рис. 5.4).
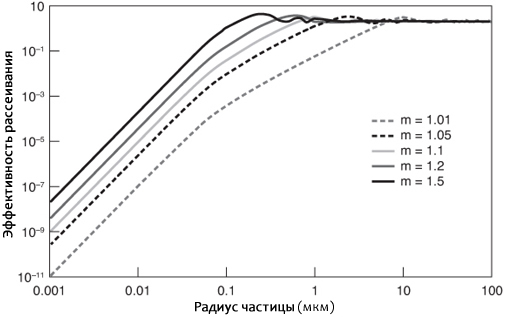
После некоторых извержений вулканов и лесных пожаров небо заполняется частицами этого диапазона размеров, и заходящее солнце и луна становятся голубыми, а не красными, поскольку красный цвет рассеивается больше, чем синий. Светорассеяние также становится более направленным вперёд при увеличении размера частиц в этом диапазоне, но опять же, есть неожиданные отклонения. Форма частиц также играет более значимую роль, и результат может быть трудно предсказать.
Единственный ответ на всё это – использовать компьютер. Густав Ми разработал точное решение для расчёта рассеяния на сферах любого размера в 1908 году. Фактически его подбил на это Лоренц, который, к сожалению, публиковался на датском языке, а на нём мало кто читал в то время. Петер Дебай также сыграл свою роль, поэтому, чтобы физики-оптики были счастливы, лучше всего называть эту теорию «теорией Лоренца-Ми-Дебая» (см. Bohren and Clothiaux, 2006, для обсуждения этого). Ми, однако, первым применил теорию для решения реальной проблемы – объяснения цвета знаменитого богемского рубинового стекла, который, как оказалось, обусловлен сложной комбинацией поглощения и рассеяния света включёнными в стекло частицами золота размером 10 нм. Однако, как бы вы его ни называли, само уравнение растянуто на много страниц, и его трудно решить без компьютера. Тот факт, что довольно большое количество случаев было разрешено в предэлектронный период расчётов, является свидетельством того, как тяжело работали тогда люди. Сейчас можно легко найти бесплатные пакеты программного обеспечения, работающие на любой платформе. Хотя теория Ми была разработана для сферических тел, она дает достаточно точные результаты для любого грубо сфероидального объекта (например, средней органеллы или фитопланктона). Существуют также точные решения для плоских поверхностей и длинных цилиндров – эти три (включая сферу), являют формой большинства биологических объектов. Существуют даже строгие решения для концентрически наслоенных сфер, которые полезны в случае клеток, где ядра, цитоплазма и плазматическая мембрана имеют разные показатели. Если интересующая вас частица действительно причудлива по форме, то вам нужно использовать методы конечных элементов или другой метод непосредственного решения уравнений Максвелла.
Конечно, недостатком использования компьютера является то, что вы теряете интуитивное понимание того, что имеет значение при рассеянии. Несколько шаблонов происходящего при рассеивании на малых частицах актуальны и для больших. Например, рассеяние по-прежнему пропорционально (m-1)2 в частицах с диаметром до двух длин волн. В общем случае поперечное сечение рассеяния и углы рассеяния света зависят от размера, формы и показателя сложными способами. Для некоторых особых случаев существуют несколько более простых формул, разработанных отчаянно желавшими упростить вычисления исследователями в докомпьютерную эпоху, но они недостаточно просты, чтобы предлагать любое реальное понимание, поэтому уж лучше с компьютером.
Укрывистость
Что насчёт показателя преломления? Как видно из рисунка 5.4, когда частица становится достаточно большой, количество рассеянного света не зависит от показателя преломления. Если это вас не волнует, то должно. Точно ли алмаз (n = 2,4) рассеивает больше света, чем стекло (n = 1,5)?
Оказывается, что, хотя показатель преломления не влияет на то, сколько света рассеивается в больших частицах, он влияет на то, где он рассеивается. По мере того как частицы становятся больше, они рассеивают всё больше и больше света по направлению вперёд. Это связано с волновой интерференцией, о которой мы поговорим подробнее в следующей главе. Однако для частиц с высоким показателем этот эффект наступает медленнее. И зачем нам это принимать во внимание?
В биологии, как правило, предмет интереса состоит том, сколько и где рассеивается света. Например, репница (Pieris rapae, родственница капустницы) имеет белые крылья. Под электронным микроскопом можно увидеть, что чешуйки белых участков крыльев покрыты хитиновыми бусинками (n ≈ 1,56) диаметром 100-500 нм (Stavenga et al., 2004) (рис. 5.5). Чёрные области крыльев не имеют бусинок, что заставило авторов предполагать, что бусины отвечают за белый цвет. Если да, то это оттого, что бусины рассеивают много света или потому, что они рассеивают его на большие углы? Более конкретно, если бы у вас был фиксированный объём хитина для работы, как бы вы его разделили, чтобы отразить побольше света? Несколько больших бусин? Много крошечных?

Аналогичная проблема заботит лакокрасочную промышленность. Белая краска белая, поскольку она содержит небольшие кристаллы диоксида титана в прозрачной латексной основе. Оксид титана имеет показатель преломления между 2,4 и 2,6, поэтому он хорошо рассеивает свет. Однако это дорого, поэтому разработчики красок хотят найти кристалл с таким размером, который позволить рассеивать максимальное количество света на объем, и рассеивать его во всех направлениях.
В большинстве случаев, когда что-то зависит от двух параметров, результат обоих параметров является хорошим способом подумать об оптимизации процесса. Эта задача не исключение. Результат, используемый разработчиками краски:
5.10
где g - параметр асимметрии, о котором мы говорили. Получившийся H иногда называют «средневзвешенным угловым рассеянием», но мне нравится термин, применяемый для него в лакокрасочной промышленности: «укрывистость» (потому что краска скрывает то, что находится под ней). Поскольку g сильно зависит от показателя преломления, то, хотя крупные частицы и имеют одинаковое эффективное поперечное сечение, вы заметите разницу в укрывистости между краской, полученной из алмазных частиц, и краской, сделанной из стекла.
Как я уже упоминал, обычно люди (и природа) заботятся о том, чтобы максимизировать что-либо, данное в ограниченном количестве, в этом случае ограничен объём. Так что Dupont (и естественный отбор для белой бабочки) заботятся об ограниченной объёмом укрывистости, или H/V. Если исследуемые частицы не имеют причудливой формы, она оказывается пропорциональной:
5.11
Большие частицы рассеивают много света, но рассеивают большую его часть вперёд, а это означает, что g близко к одному, что делает 1-g маленьким. Кроме того, r становится большим и находится в знаменателе, поэтому ограниченная объёмом сила низка. Маленькие частицы рассеивают свет во всех направлениях (g = 0), но невероятно неэффективны, поэтому ограниченная объёмом укрывистость снова низка. Итак, где же наилучшее значение? Достаточно хорошим ответом являются частицы, чей диаметр находится между половиной, а также равный длине волны света, причём показатель преломления частиц не имеет значения (рис. 5.6). Разбейте любое не поглощающее вещество на частицы такого размера, и оно станет хорошим белым веществом. Возвращаясь к бабочке, частицы диаметром 100-500 нм, содержащиеся на их белых крыльях, имеют правильный размер, чтобы рассеивать видимый свет во многих направлениях. Бусины диаметром два микрометра были бы только наполовину эффективны.
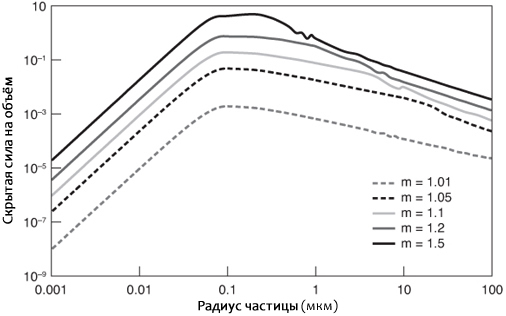
Прежде чем мы перейдём к рассеиванию на множестве частиц, я хотел больше рассказать о важности размера частиц. Как я уже упоминал, укрывистость на объём достигает пика, когда вещество разбивается на частицы с радиусами вблизи длин волн падающего света. По обе стороны от этого пика находится крутые склоны, на которых укрывистость падает на много порядков. Хотя масштаб размеров разный, мне нравится думать об этом как об эффекте «дроблёного льда». Предположим, вы добавили определенный объём льда в стакан воды. Если лёд разбит на микроскопические кристаллы, то общее рассеяние на каждом кристалле будет небольшим (игнорируйте тот факт, что мелкие кристаллы сразу бы растворились). Если бы вы бросили в стакан два больших кубика льда, то всё равно могли бы видеть сквозь стекло достаточно хорошо. Каждый кубик сам по себе рассеивает много света, но их всего два, поэтому относительно общего объёма поступающего света они не рассеивают много. Однако, если вы раздробите кубики, вы едва сможете видеть сквозь стекло стакана. У вас правильная комбинация высокого рассеяния на частицу и количества частиц.
Этот же процесс объясняет, почему вы можете видеть сквозь дождь, но не сквозь туман. Объемная плотность воды в тумане на самом деле довольно низка, но если вы когда-либо ехали через туман, то знаете, что он хорошо рассеивает свет. Тем не менее, вы можете легко ехать при умеренно сильном дожде, хотя объемная плотность воды в воздухе в этом случае намного выше. Это связано с тем, что укрывистость на объём для капель воды, составляющих туман, намного выше чем у капель воды, размер которых позволил им стать дождём. Когда я жил во Флориде, у нас были предсказуемые и сильные грозы во второй половине дня. Они почти всегда начинались с драматического потемнения неба, но сам дождь обычно не начинался, пока небо не становилось светлее. Это связано с тем, что центр грозы по существу является многокилометровой колонной падающего дождя. Дождь, хотя и более плотный, чем облака, рассеивает меньше света, и соответственно, пропускает его больше. Если вы живете в районе с сильными грозами, вы можете произвести впечатление на своих друзей используя движение более светлой области тучи для предсказания, когда начнёт падать дождь.
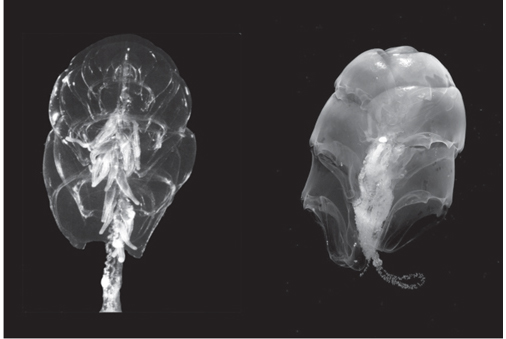
Есть также несколько животных, контролирующих размер частиц внутри их тел для влияния на рассеяние света. Большинство из них – сифонофоры, но я также видел эффект у некоторых крылоногих. Все эти животные в норме являются прозрачными, но становятся белыми через несколько секунд после того, как вы их коснётесь. Очень интересно погружаться с этими животными, и касаясь их, наблюдать как они вскрываются. Наиболее изученными из делающих это видов является сифонофор Hippopodius hippopus (рис. 5.7). Джордж Маки работал над ними в 1960-х годах и обнаружил, что их увеличивающаяся непрозрачность обусловлена осаждением белка в пределах мезоглеи животного. В растворенном состоянии белки имели малое объёмное рассеяние. Однако после осаждения более крупные частицы имели более высокое удельное объемное рассеяние и делали животное непрозрачным. Почему эти животные, по-видимому, сознательно превращаются в непрозрачных, когда их беспокоят, остаётся только догадываться.