Квантовая запутанность
Возможно, самым странным аспектом квантовой механики является то, что было названо «запутанностью». В то время как эксперимент на двух щелях хотя бы частично можно объяснить с помощью различных интуитивных аргументов, поведение запутанных фотонов оставляет всех в недоумении. Как однажды сказал Дэвид Мермин, запутанность настолько близка к магии, насколько вообще в физике есть место для магии (Mermin, 1985). Мермин также цитирует неназванного физика, говорившего, что человека не беспокоит квантовая запутанность только если у него в голове камни (Mermin, 1985). Запутанность является довольно общим явлением, которое также существует в элементарных частицах. Однако, поскольку это книга о свете, я буду придерживаться запутанных фотонов. Просто имейте в виду, что всё нижеизложенное не является специфическим для света и поляризаторов, но является общим аспектом эффектов измерения. Другими словами, оно находится в центре всего.
Итак, начнём сначала – некоторые фотохимические процессы производят пары фотонов с коррелированными поляризациями. Другими словами, разность между углами поляризации двух фотонов постоянна. Точная разница зависит от того, как создаются фотоны, но не является критической для центральной концепции запутанности. Например, фотон, который входит в кристалл бората бета-бария (β-BaB2O4), будет иногда разделяться на два фотона, каждый из которых имеет половину энергии и удваивает длину волны исходного фотона (Dehlinger and Mitchell, 2002). Процесс, известный как «спонтанное параметрическое рассеяние», по-видимому, не имеет биологического значения, поэтому мы просто примем его и пойдём дальше. Эти новые фотоны покидают кристалл, двигаясь в противоположных направлениях, но имея одинаковую поляризацию. Про них говорят, что они запутались (образовали спутанную пару).
Тем не менее, хотя вы знаете, что поляризации двух фотонов идентичны, вы не знаете, каковы они. Они могут быть поляризованными вертикально, горизонтально, или под любым углом между ними. Давайте посмотрим, что произойдет, когда вы попытаетесь это выяснить.
Представьте, что вы построили приспособление, которое испускает фиолетовые фотоны с длиной волны 400 нм один за другим в кристалл бората бета-бария, и создаёт этим некоторое количество спутанных пар 800 нм фотонов. Для удобства предположим, что один фотон каждой спутанной пары идет вправо, а другой – влево. Мы будем их обнаруживать фотоумножителями со счётчиками фотонов.
Пока же давайте просто поместим детектор на путь идущих вправо фотонов. Включите детектор, и он обнаружит их постоянный поток. Число будет намного меньше, чем количество изначально вошедших в кристалл фиолетовых фотонов, поскольку только небольшая их часть разделится – остальные просто пройдут прямо. Теперь поместите поляризатор между кристаллом и детектором. Количество обнаруженных фотонов теперь падает на 50%. Поворот поляризатора не даст никакого результата – у вас всегда будет только половина фотонов от тех, что были раньше. Это имеет смысл, поскольку мы сказали, что поляризация фотонов является случайной, а из главы 8 известно, что случайно поляризованный фотон проходит через идеальный поляризатор ровно в 50% случаев, независимо от ориентации поляризатора. Переместите детектор и поляризатор на другую сторону кристалла, чтобы измерить идущие влево фотоны, и вы получите тот же результат.
Верните поляризатор и детектор обратно на правую сторону и поверните поляризатор так, чтобы он располагался вертикально. Как и раньше, проходит половина фотонов. Теперь возьмите второй детектор и вертикально ориентированный поляризатор и поместите его на путь левосторонних фотонов. Чтобы упростить описание, давайте условимся, что каждый детектор начнет мигать зелёным светом, когда он обнаружит фотон, и красным светом, когда он этого не сделает (рисунок 10.3). Включите всё. Теперь вы видите, что каждый раз, когда правый детектор видит фотон, левый детектор также видит один, и оба индикатора мигают зелёным. Кроме того, каждый раз, когда правый детектор не видит фотон, левый детектор также не видит его, и оба индикатора мигают красным. Вы никогда не видите сочетаний зелёного и красного света на разных детекторах. Кроме того, вы также отметили, что одновременные вспышки красного света на детекторах встречается так же часто, как и одновременные вспышки зелёного, в пределах обычного статистического отклонения.
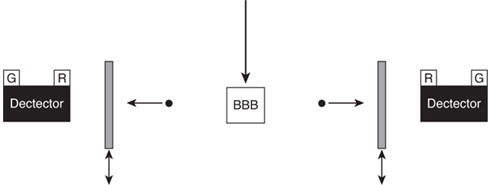
Кажется что всё в порядке, но давайте задумаемся об этом на мгновение. Предположим, что у идущего вправо фотона всегда была вертикальная поляризация. Тогда у левостороннего фотона она также существует всегда, и они оба проходят через вертикальный поляризатор. Если бы это было правдой, то индикаторы дважды мигали бы зелёным всё время. Однако мы видим, что в половине случаев индикаторы дважды вспыхивают красным светом, что означает, что ни один фотон не прошёл через тот или иной поляризатор. Поэтому они не могут быть вертикально поляризованы.
Возможно, оба фотона были поляризованы при угле 45°? Согласно закону Малюса из главы 8 они в таком случае должны пройти через вертикально ориентированный поляризатор в 50% случаев (= cos245°). Это кажется многообещающим. Однако вероятность того, что оба фотона пройдут через свои поляризаторы, составит 50% × 50% = 25%. Аналогичным образом, вероятность того, ни один не пройдёт, также составляет 25%. Таким образом, вероятность того, что индикаторы будут мигать либо красным, либо зелёным, будет 50%, а не 100%, которые мы наблюдаем в реальности. Если хотите, вы можете попробовать другие возможные углы поляризации фотонов, но обнаружите, что ни один из них не даст вам 50% двойных красных сигналов и 50% двойных зелёных, да ещё и без смешивания красного или зелёного света.
Таким образом, похоже, что прохождение одного фотона через один поляризатор каким-то образом заставляет его запутавшегося партнера пройти через другой поляризатор. Точно так же непрохождение одного фотона приводит к непрохождению другого. Установка обоих поляризаторов под одним углом является лишь частным случаем. В целом, поляризаторы могут иметь любой угол относительно друг друга, хотя это и изменяет то, как проход одного фотона влияет на проход другого. Например, если один поляризатор является вертикальным, а другой горизонтальным, то один фотон пройдёт через вертикальный поляризатор, но другой фотон никогда не пройдет через горизонтальный. В наиболее общем виде прохождение одного фотона через поляризатор изменяет шансы его спутанного собрата пройти через его поляризатор от 50% до cos2θ, где θ – разность углов двух поляризаторов. Ещё более странно то, что этот эффект «заставления» другого фотона проходить через свой поляризатор выглядит мгновенным, или, по крайней мере, он происходит со скоростью, намного превышающей скорость света. Опытные эксперименты на расстояниях в сотни метров доказали это (Salart et al., 2008). Эффект не имеет ничего общего с нелинейным кристаллом, который является просто удобным способом создания спутанных фотонов. Он также не относится к свету, хотя легче всего эффект запутанности демонстрируется с помощью фотонов и поляризаторов. По сути мы говорим о том, что измерение одного объекта может повлиять на измерение другого, мгновенно и, возможно, на огромных расстояниях. Можно понять, почему Эйнштейн называл это «жутким дальнодействием».
Единственный способ избежать этой жути – предположить, что фотоны несут наборы инструкций, говорящий им что делать при любой ориентации поляризатора. Например, «Если поляризатор установлен на 45°, всегда проходите, если он установлен на 0°, никогда не проходите» и т.д. Наборы инструкций, вообще-то говоря, были бы разными для разных фотонов (то есть, фотоны приходили бы в разных видах), но два фотона спутанной пары несли бы одни и те же инструкции. Это называется гипотезой «скрытых параметров». Это странная идея, но не страннее и истиннее «целующихся кузенов» в квантовой механике. Кроме того, никто не смог придумать какою-либо другую идею, сохраняющую хотя бы отдалённое интуитивное чувство реальности. Попробуйте, может у вас получится.
Дискуссия между жутким дальнодействием и скрытыми параметрами была начата Эйнштейном, Борисом Подольским и Натаном Розеном в 1934 году (Einstein et al., 1934) и быстро стала известна как парадокс Эйнштейна-Подольского-Розена. Она оставалась философской дискуссией, пока Джон Белл не нашёл экспериментальный способ выделить два параметра (Bell, 1964). Документ содержит всего шесть страниц, но не очень доступен для нефизиков. Однако основные идеи просты и прекрасно объясняются другими учёными. Следующее близко к тому, что дал Дэвид Мермин (David Mermin, 1985).
Мы будем использовать наш оригинальный аппарат с его фиолетовым светом, нелинейным кристаллом, парой поляризаторов и подсчитывающих фотоны детекторов с красными и зелёными индикаторами, но к каждому из наших двух поляризаторов добавим устройство, случайным образом поворачивающее их на одну из трёх ориентаций: 0° (вертикально), 120° или -120°. Ориентации двух поляризаторов независимы друг от друга и выбираются случайным образом каждый раз, когда источником света испускается новый фиолетовый фотон (рис. 10.4). Точное время изменения ориентации не имеет значения, если это происходит до того, как фотоны пройдут через них. Чтобы всё было проще, мы предположим, что фотоны испускаются с постоянной скоростью и что каждый фотон, входящий в кристалл, расщепляется.
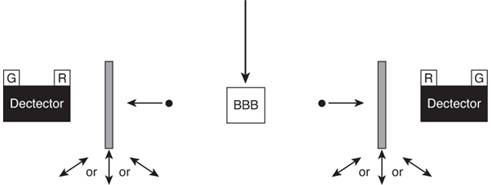
Включите всё и пустите пучок фотонов через систему. Вы обнаружите, что в среднем огни индикатора мигают красный-красный, зелёный-зелёный, красный-зелёный и зелёный-красный в равной пропорции (каждая по четверти от общего времени). В частности, вы обнаружите, что половину времени загораются два индикатора одного цвета, и половину времени загораются индикаторы разных цветов. Однако вы также увидите, что, когда два поляризатора имеют одинаковую ориентацию (оба вертикально, 120° или -120°), оба индикатора всегда будут мигать одним и тем же цветом. Когда углы двух поляризаторов отличаются друг от друга, индикаторы мигают одинаковым цветом только одну четверть от общего времени. Оба этих состояния могут быть объяснены описанным выше законом квадрата косинуса. Треть времени два поляризатора ориентированы под одинаковым углом, поэтому cos2θ = 1, что означает, что либо оба фотона проходят, либо нет. Остальные две трети времени поляризаторы ориентированы под разными углами. В этом случае угол между ними всегда равен 120° или -120°, поэтому cos2θ = 1/4, а индикаторы мигают одинаковым цветом только четверть от общего времени. Сложите два случая вместе, и вы получите `1/3 * 1 + 2/3 * 1/4 = 1/2`, что означает, что индикаторы должны мигать одинаковым цветом половину времени, и это соответствует тому, что мы видим. Пока всё идет нормально.
Предположим, что гипотеза о скрытых параметрах истинна. Существует три ориентации поляризатора, поэтому набор инструкций должен сообщать фотону, что делать в каждом случае. Для каждой ориентации фотон мог либо пройти, либо нет, что означает, что существует восемь возможных наборов команд (= 23). Возможный набор команд может состоять в том, чтобы фотон всегда должен проходить через вертикальный поляризатор, всегда проходить через поляризатор под углом 120° и никогда не проходить через -120 °. Назовем эту инструкцию GGR (green-green-red) – сокращения от зелёный, зелёный и красный сигналы индикатора, которые будут мигать для поляризаторов, ориентированных соответственно на 0°, 120° и -120°.
Поскольку два спутанных фотона всегда вызывают мигание одинаковых индикаторов в случае, если оба поляризатора имеют одинаковую ориентацию, они должны иметь одинаковые наборы команд. Тем не менее, у нас с этим проблемы, поскольку два индикатора мигают одинаковым цветом в 50% случаев. Давайте посмотрим, почему. Два набора инструкций, а именно RRR и GGG, каждый раз вызывают мигание одинаковым цветом. Как насчет остальных шести? Давайте снова возьмем GGR для примера. Существует девять возможных пар ориентаций поляризаторов (таблица 10.1). Вы можете видеть, что для этого набора правил оба индикатора мигают тем же цветом 5/9 времени. Основная причина этого заключается в том, что один цвет (зелёный) в наборе команд встречается дважды, а другой встречается только один раз. Остальные пять наборов правил будут иметь ту же проблему: один цвет всегда будет встречаться дважды, а другой – только один раз. Если хотите, можете проверить, но вы всегда обнаружите что индикаторы будут мигать одним и тем же цветом 5/9 времени. Объедините это с тем фактом, что фотоны с наборами инструкций RRR и GGG всегда мигают одним цветом (есть только один цвет для индикатора), и вы обнаружите, что если бы два запутанных фотона имели один и тот же набор команд, то два детектора должны мигать одинаковым цветом не менее 5/9 времени, что больше, чем наблюдаемые 50%.
| Левый | Правый | Цвета (левый/правый) |
|---|---|---|
| 0 | 0 | GG |
| 0 | 120 | GG |
| 0 | -120 | GR |
| 120 | 0 | GG |
| 120 | 120 | GG |
| 120 | -120 | GR |
| -120 | 0 | RG |
| -120 | 120 | RG |
| -120 | -120 | RR |
Этот эксперимент был проведен много раз во многих лабораториях (даже в студенческих учебных лабораториях), и конечный результат заключается в том, что одни и те же цвета вспыхивают значительно меньше 5/9 времени (обычно меньше как минимум на десять стандартных отклонений). Поэтому гипотеза скрытых параметров не может быть правдой. А это означает, что просто процесс прохождения одного фотона через поляризатор влияет на поляризацию родственного, но, по-видимому, в остальных отношениях независимого фотона на больших расстояниях. Другими словами, свойства объекта каким-то образом зависят от того, что происходит в других местах.
Эксперимент проводился на всё более увеличивающихся расстояниях. Текущая зафиксированная дистанция составляет не менее 50 километров, и при проведении эксперимента использовались фотоны, передаваемые через оптические волокна (Marcikic et al., 2004). На открытом воздухе фотоны подвержены на своём пути влиянию окружающей среды, поэтому дистанция короче, но по-прежнему составляет не менее 600 метров (например, Aspelmeyer et al., 2003). Другие эксперименты протестировали скорость эффекта и обнаружили, что она по меньшей мере в 10 000 раз превышает скорость света (Salart et al., 2008).
Если все другие странности света не беспокоят вас, то квантовая запутанность действительно должна. Тем более, как я уже говорил, речь идет не только о свете, но и обо всей материи. Подобные эксперименты были выполнены с использованием спутанных элементарных частиц, спины которых измерялись с использованием магнитов. Эксперименты сложнее в проведении, но дают те же результаты. Это также не о поляризаторах или магнитах, а о самом процессе измерения. Мы начали эту главу с принципа неопределенности, который гласит, что нельзя измерить свойства малых объектов с произвольной точностью (неограниченным количеством значащих цифр). Я сказал, что это понятно, поскольку само измерение нарушит объект (пример с плотвой и битой). Но каким образом измерение одного фотона влияет на другой фотон, находящийся за мили от него?
На данный момент ответа на этот вопрос нет. Одна из возможностей заключается в том, что существует некоторая неизвестная сила, которая перемещается от измеренного фотона к его спутанному партнеру со скоростью, по меньшей мере, в 10 000 раз превышающей скорость света. Другая возможность заключается в том, что пространства не существует, по крайней мере, не в том виде, как мы о нём думаем. Хотя мы можем думать о двух спутанных фотонах, как о находящихся на расстоянии друг от друга, на более фундаментальном уровне они могут находиться в одном и том же месте. Я лично предпочитаю эту гипотезу. Она ясная, и достаточно ненормальная, чтобы быть правдой. Она также, по крайней мере для меня, хорошо согласуется со специальной теорией относительности. Одна из центральных догм относительности состоит в том, что вы не можете сказать, что два события произошли действительно одновременно. Вместо этого их относительное время зависит от движения наблюдателя относительно двух событий. Возможно, в квантовой механике мы также не можем сказать, действительно ли две вещи находятся в одном и том же месте, или нет.
И пока мы говорим об относительности, важно отметить, что такие извороты как запутанность не нарушают принципов специальной теории относительности. Это правда, что влияние измерений движется намного быстрее, чем скорость света, и может быть фактически мгновенным. Но вы не можете использовать его для отправки сигнала. Предположим, вы сидите рядом с одним из детекторов нашего устройства, а ваш друг находится в нескольких милях, и сидит рядом с другим детектором. Если бы вы могли контролировать, проходит ли фотон через ваш поляризатор или нет, вы могли бы повлиять на фотон, который видит ваш друг. Изучите код Морзе, и вы сможете общаться на скорости, значительно превышающей скорость света. К сожалению, вы не можете контролировать прохождение фотона через ваш поляризатор. В среднем он делает это только половину времени. Для любого конкретного фотона это подбрасывание монетки. Таким образом, вы не можете отправить целенаправленный сигнал, и поэтому теория относительности не нарушается.
Тем не менее, поскольку на спутанные фотоны влияет измерение, этот факт можно использовать для определения прослушивания линии связи. Это основа так называемой «квантовой криптографии» – термин слегка некорректный, поскольку система является не кодом, а способом определить, было ли изменено сообщение. Возможно сломать даже наиболее защищённые коды, если у вас есть ключ. И проблема, таким образом, заключается в безопасной передаче ключа. Можете зашифровать ключ, но тогда нужно беспокоиться о безопасной передаче ключа для ключа – и т.д. На практике невозможно отправить ключ полностью безопасным способом. Но можно осуществить следующий лучший вариант. Используя систему спутанных фотонов, возможно по крайней мере определить, пытался ли кто-нибудь прочитать ключ во время передачи. Любая попытка перехвата передачи по существу является измерением, и будет влиять на корреляции между поляризацией спутанных фотонов. Если замечено изменение, ключ считается скомпрометированным, и предпринимается другая попытка отправки. Насколько известно, невозможно перехватить ключ, отправленный с помощью квантовой криптографии так, чтобы это осталось незамеченным.
Такие системы существуют. Начиная с 2004 года некоторые банковские транзакции высокого уровня и небольшие компьютерные сети используют квантовую криптографию, и несколько компаний производят и продают такие системы. Текущие дистанции составляют около 200 километров для волоконно-оптических систем и 150 километров для систем под открытым небом. Лично у меня нет секретов, требующих разрыва ткани Вселенной чтобы их обнаружить, но меня никогда не перестаёт удивлять, как даже самую туманную науку можно продать через компании с названиями типа ID Quantique, MagiQ Technologies, SmartQuantum, и Quintessence Labs. Очевидно, это все о Q.
Конец пути
Таким образом, мы прошли долгий путь от наших начальных проблем с единицами и геометрией. Возможно, больше, чем любая другая область науки, наше желание понять свет открыло целые миры – от открытия Ньютоном цветов, находившихся в белом свете, до исследований девятнадцатого века, в конечном счете показавших что электричество, магнетизм и свет были тесно связаны, и, наконец, к изменяющему разум двойному перевороту специальной теории относительности и квантовой механики. Есть те, кто впечатлён цифровой точностью квантовой механики, и считают, что это путешествие, каким бы захватывающим оно ни было, подошло к концу.
Полагаю, скорее всего так и есть. В то время как новые вещи о свете открываются постоянно, в течение многих десятилетий не произошло ничего фундаментально нового, сопоставимого с появлением квантовой механики, несмотря на беспрецедентное количество работающих в этой области умных и хорошо финансируемых людей. Однако мне очень хочется надеяться, что ещё одно простое озарение может открыть ещё один новый мир. В конце концов, теория относительности Эйнштейна развивалась из его простой идеи: «Если я поставлю зеркало на свой велосипед и поеду достаточно быстро, исчезнет ли мое отражение?» Эксперименты, конечно, тоже имеют критическое значение, но никогда не нужно сомневаться в том, что сила простой идеи способна перевернуть мир.
В детстве я читал одну книгу. Я не помню названия или даже того, что в ней произошло. Всё что я помню, это мальчика, который мог входить в четвёртое измерение. Ему не требовалось никакого специального оборудования – он просто поворачивался в правильном направлении. Я часто о нём думаю, и представляю себе огромный невидимый мир, может быть находящийся в сантиметрах от наших лиц и умов, скрытый, пока один из нас просто не научится правильно смотреть.

