Частота против длины волны
Как я сказал ранее, произведение длины волны и частоты равно скорости света. Здесь есть два осложнения. Во-первых, есть несколько определений скорости света. Мы обсудим это далее в главе 5. Пока остановимся на том, что «скорость» означает фазовую скорость, являющуюся скоростью, с которой движутся волновые гребни изменяющихся электрических и магнитных полей вдоль заданного направления. Второе осложнение состоит в том, что фазовая скорость зависит от среды, через которую проходит свет. Более конкретно, произведение λ и ν равно скорости света в вакууме (c), делённому на показатель преломления среды (n). Другими словами, λν = c/n.
Итак, предположим, что луч солнца исходит из воздуха (n ≈ 1) в океан (n ≈ 1,33). Индекс преломления растёт, поэтому фазовая скорость падает в 1,33 раза. Так как скорость является произведением частоты и длины волны, также должен упасть один из этих показателей (или оба). Оказывается, частота остается неизменной, а уменьшается длина волны. В этом случае «зёленый» фотон 550 нм в океанской воде фактически имеет длину волны 414 нм. Таким образом, частота выглядит более фундаментальным показателем, чем длина волны. Кроме того, помните, что энергия фотона пропорциональна частоте, но не длине волны (формула для преобразования ватт в фотоны в предыдущем разделе работает только в том случае, если вы используете длину волны, которую свет будет иметь в вакууме). Это важно, потому что во многих процессах, таких как поглощение, важна энергия фотона, а не длина волны. Например, длина волны «зёленого» фотона внутри нашего глаза будет завесить от того, наполнен ли глаз водой или воздухом (разный индекс преломления), но наше восприятие цвета от этого не изменится, поскольку поглощение света фоторецепторами зависит от энергии фотонов, а она связана с остающейся неизменной частотой.
Однако, как я уже говорил, люди предпочитают единицы длины над единицами частоты (по крайней мере, я сам так делаю). Кроме того, ранняя история оптики больше фокусировалась на явлениях, которые лучше объяснялись мышлением о длине волны (интерференция, дифракционные решётки и т.п.). Родственные вопросы об энергии фотонов и электронных уровнях не появлялись до начала XX века. Наконец, длины волн видимого спектра света являются небольшими, и измеряются, от 0,4 до 0,7 мкм. Соответствующие этим длинам волн частоты составляют порядка 1014 Гц, и с трудом поддаются измерению. Чтобы дать вам представление о величине этой частоты, представьте, что секунда растянута на период в сто лет. Световая волна же по-прежнему будет проходить полный цикл за 3/100 000 (нормальных) секунд. Итак, если вы не работаете на границе биологии и квантовой физики, я бы настоятельно предложил вам придерживаться длин волн, что буду делать и я в этой книге.
Прежде чем расстаться с частотой навсегда, необходимо обсудить одну важную проблему. Она связанна с тем фактом, что спектр света является гистограммой. Предположим, вы измеряете спектр дневного света и что значение для длины волны 500 нм составляет 15 фотонов/см2/с/нм. Это не означает, что имеется 15 фотонов/см2/с с длиной волны ровно 500 нм. Это означает, что существует интервал шагом в 1-нм, центрированный на длине волны 500 нм, и на его протяжении у вас есть 15 фотонов/см2/с. Интервалы гистограммы спектра не обязательно должны быть шириной 1 нм, но все они должны иметь одинаковую ширину (шаг).
Предположим, что все интервалы имеют ширину 1 нм и шаг в целых числах (т. е. один на 400 нм, один на 401 нм и т.д.). Что произойдет, если мы преобразуем эти значения длины волны в их частотные соответствия? Выберем длины волн двух соседних интервалов и назовем их λ1 и λ2. Соответствующие частоты ν1 и ν2 равны c/λ1 и c/λ2, где c - скорость света. Мы знаем, что λ1 - λ2 равны 1 нм, но чему равны ν1 - ν2?
2.1
Вы можете сделать последний шаг, потому что λ1 близка к λ2. Таким образом, ширина интервалов частот зависит от соответствующим им длин волны, что означает, что они не будут равны! На самом деле они весьма неравны. Интервалы на красном конце спектра (700 нм) будут составлять всего лишь треть от ширины интервалов на синем конце (400 нм). Это означает, что спектр, созданный с использованием равных интервалов для частот, будет отличаться от спектра с равными интервалами длины волны. Итак, какой из них правильный? Ни тот, ни другой. Смысл в том, что фигура спектра зависит от того, используете ли вы одинаковые размерности шага для частоты или для длины волны.
И почему всё это должно вас волновать? Ведь можно всё сделать, просто используя длину волны? К сожалению, не все функции, построенные по длине волны, являются гистограммами. Кривые зрительной чувствительности, спектр повреждения от ультрафиолетового излучения – всё в этом роде – известны как «точечные функции» и не подвержены эффекту интервалов. Это может привести к серьёзному неправильному толкованию. Например, существует давняя уверенность в том, что зрительная чувствительность человеческого глаза оптимизирована для восприятия дневного света. Уверенность основана на том факте, что зрительная чувствительность нашего дневного зрения достигает максимума при свете с длиной волны 555 нм, а максимум дневного света приходится на длину волны около 510 нм. Звучит складно, не так ли?
Прежде всего, кривая нашей зрительной чувствительности всегда указывается в единицах отклика на ватт, так же как и дневной свет обычно даётся в ваттах, несмотря на тот факт, что наши глаза фиксируют не энергию, а фотоны. Если преобразовать кривую чувствительности к отклику на фотон, а спектр дневного света в фотоны/см2/с, пик чувствительности теперь будет приходиться на длину волны 550 нм, а максимум дневного света окажется около 685 нм соответственно. Это не слишком хорошо, но всё же не слишком противоречиво, так? Однако, если вы измеряете спектр дневного света с использованием фотометра, настроенного на идентичные интервалы частот, пик дневного света теперь приходится на область около 1600 нм (рис. 2.3). Это далеко в инфракрасной зоне и нигде вблизи нашей кривой зрительной чувствительности.
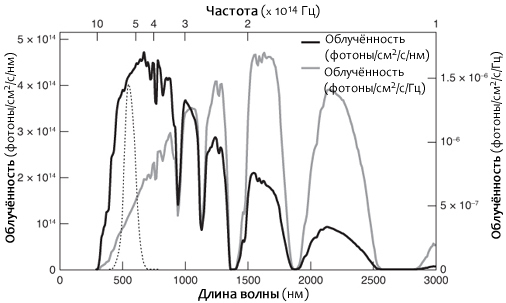
Итак, какой спектр дневного света является корректным относительно кривой чувствительности человеческого глаза? Как мы упоминали выше, вероятность поглощения фотона фоторецептором глаза зависит от частоты, а не длинны волны. Отсюда можно вывести аргумент, что при построении спектра оправданно использование интервалов частот. Однако правильный ответ заключается в том, что сравнение положения пиков бессмысленно. Можно сравнивать пики на спектре один с другим, при условии, что они получены с использованием одинаковых интервалов, будь то длина волны или частота. Но нельзя сравнивать их с спектрами действия и кривыми зрительной чувствительности, поскольку последние являются точечными функциями, а не гистограммами, и потому не зависят от того, что отложено по оси X – частота или длина волны. Единственный раз, когда это допустимо, это в случае, когда весь свет имеет почти одинаковую длину волны, как в толще воды. Тогда пик остаётся на месте (более или менее), независимо от того, работаете ли вы с интервалами длин волн или частотой. Однако за пределами глубокого моря вы почти никогда не увидите такого узкого спектра.
И что с этим можно сделать? Оказывается, что хотя пики гистограммы зависят от того, на какие интервалы разбиты данные, на общий массив данных это не влияет. Это можно доказать расчётами, но вместо этого просто подумайте о том, что складываете сто стеклянных шаров в десять вёдер различного размера. Независимо от того, как вы разделите шарики между вёдрами, у вас всегда будет сто шаров. Поэтому чтобы узнать, действительно ли зрительная система человека оптимизирована для дневного света, нужно взглянуть на общий объём поглощённого света со всеми длинами волн, и так ли он велик, как мог бы быть. Мы сделаем это подробно в главе 4, которая охватывает поглощение.
Важным следствием проблемы фотонов/энергии и длины волны/частоты является то, что вы не можете однозначно сказать, что свет является спектрально нейтральным (он же «белый»). Речь идёт не про тот факт, что наши визуальные системы воспринимают разнообразный спектр длин волн как белый цвет («цветопостоянство»), но о том, что способ отображения спектра зависит от используемых вами единиц, и от того, как вы разделяете данные. Другими словами, спектр, имеющий одинаковое количество энергии в каждом интервале длин волн, не будет иметь одинакового количества фотонов в том же интервале длин волн. Кроме того, оба этих спектра будут выглядеть совершенно по-другому, если вы перестроите их, используя аналогичные интервалы частот. Таким образом, практически ни один из реальных источников света не приближается к тому, чтобы быть спектрально плоским ни в одном из этих четырёх механизмов, но среди занимающихся светомоделированием общепринято допускать, что существует спектрально плоский источник «белого» света. Это, конечно, можно делать, но стоит помнить, что результаты не имеют универсального значения. Спектр будет плоским только для единиц и интервалов, которые вы выберете для работы.

